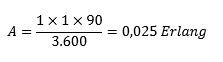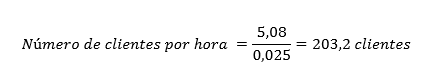Matemáticas aplicadas a las centrales telefónicas

David Ortega Sicilia, padre de una de mis alumnas al que agradezco su apoyo y la cantidad de aportaciones que me hace, ha tenido la amabilidad de enviarme esta entrada sobre matemáticas aplicadas a las centrales telefónicas:

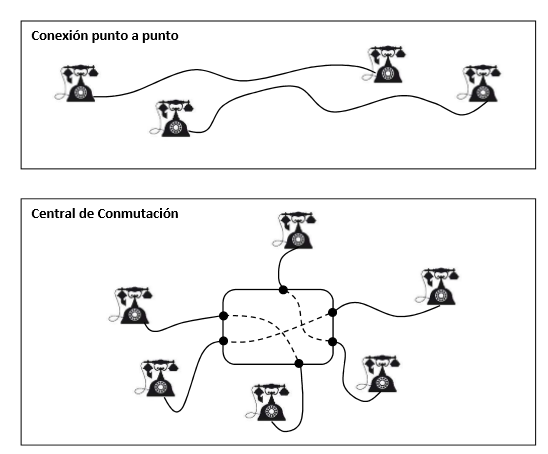
Poco tiempo después de la aparición del teléfono por parte de su verdadero inventor, Antonio Meucci (erróneamente atribuido durante décadas a Graham Bell), se instalaron las primeras líneas punto a punto donde se conectaban los terminales por parejas, permitiendo que dos usuarios por línea pudieran comunicarse entre sí. Esta distribución limitaba las posibilidades de comunicación entre múltiples usuarios, por lo que el siguiente paso fue llevar todas las líneas a una central que disponía de los medios suficientes para conectar un teléfono con cualquier otro sin necesidad de estar agrupados por parejas. Estos medios son los que constituyen los elementos de conmutación, siendo una parte fundamental de la red telefónica.

En 1978 se puso en servicio la primera central de conmutación en New Haven, Estados Unidos. Atendía a un total de 21 usuarios mediante la conexión manual de clavijas por parte de una operadora. Pero el número de clientes creció con gran rapidez, por lo que el tamaño de las centrales telefónicas aumentó hasta llegar a los 10.000 clientes atendidos, alcanzando los límites técnicos y prácticos para este tipo de sistemas. Comenzó así una nueva era tecnológica, donde la conmutación se realizaba con elementos electromecánicos y ya no era necesaria la intervención humana. Para automatizar la conexión entre dos teléfonos fue necesario proporcionar una numeración a cada abonado.

De este modo, el establecimiento de una llamada comenzaba con la marcación del número de teléfono de la persona con quien se deseaba hablar.

La tecnología fue avanzando para dar respuesta al constante crecimiento del número de abonados, pasando así por los sistemas semielectrónicos, electrónicos y digitales en los que al servicio de voz se le han añadido los datos para permitir la conexión a Internet. El transporte de la señal del teléfono también ha evolucionado desde las costosas líneas de cobre hasta las modernas redes de fibra óptica, donde se permiten grandes velocidades en la transmisión de la información como por ejemplo la señal de televisión, al tiempo que se reduce notablemente los costes de mantenimiento de la red y se mejora la eficiencia energética de todo el sistema.

Planteamiento del problema

Pero hay algo en común que perdura desde las primeras operadoras que enchufaban las clavijas en la línea deseada, hasta los sistemas más modernos. Se trata del cálculo del número de recursos de conmutación que necesita una central para atender a un determinado grupo de clientes. Si por ejemplo, en una población hay 1.000 abonados, ¿cuántas operadoras o circuitos de conmutación debemos tener en nuestra central? La respuesta rápida sería 500 para conectar la mitad de los teléfonos con la otra mitad. Pero no es correcto porque todos los clientes no llaman a la vez por teléfono en condiciones normales. Entonces, ¿cuántos recursos debe tener la central telefónica?

El estudio de la cantidad de recursos necesarios para atender a una población se llama dimensionado. Para ello, necesitamos saber cuál es la probabilidad de que un cliente realice una llamada en un tiempo determinado (por ejemplo en una hora). Además, necesitamos saber cuánto dura esa llamada. Si cada cliente hace una llamada de 1 minuto de media, entonces en una hora un circuito de conmutación podrá dar servicio a 60 clientes (1 hora = 60 minutos).
Veamos a continuación cuál es la probabilidad de realizar llamadas y como afecta la duración de las mismas.

Distribución de Poisson

Si tiramos un dado muchas veces y apuntamos el número de veces que se sale en cada tirada, al final todos tienen 1/6 de probabilidad de salir. Es decir, como el dado tiene 6 caras, cada cara saldrá 1/6 de las veces.
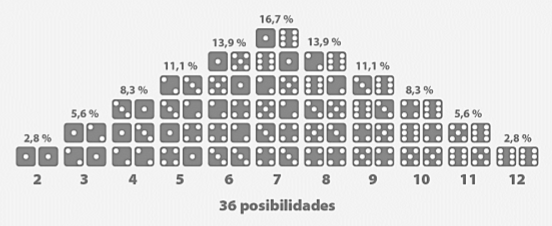
Si ahora tiramos dos dados, nos pueden salir varias combinaciones:
– un 2 solo puede salir con dos unos

– un 3 puede salir con un uno en un dado y un dos en otro, y viceversa

– un 4 puede salir con uno y tres, dos y dos, tres y uno.

– etc.

Como podemos ver, hay más combinaciones de dados para obtener un 7 que cualquier otro número. Es decir, el 7 tiene más probabilidad de salir que los demás.

Ahora que entendemos mejor el concepto de probabilidad, ¿qué pasa con las llamadas telefónicas?

La distribución de Poisson fue desarrollada por Siméon‐Denis Poisson (1781‐1840). Esta distribución de probabilidades es muy utilizada para situaciones donde los sucesos son impredecibles o de ocurrencia aleatoria. No sirve para el ejemplo de los dados, pero puede describir:
• El número de autos que pasan a través de un cierto punto en una ruta durante un periodo definido de tiempo.

• El nº de llamadas de teléfono/min en una central telefónica.

• El número de servidores web accedidos por minuto.

• El número de mutaciones de determinada cadena de ADN después de cierta cantidad de radiación.

• El número de defectos por metro cuadrado de tela.

• El número de estrellas en un determinado volumen de espacio.

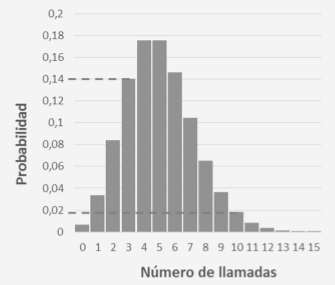
En la siguiente gráfica vemos un ejemplo de la probabilidad de que se produzca una cantidad x de llamadas durante un minuto, según la distribución de Poisson.

Según vemos, la probabilidad de que ocurran 3 llamadas en un minuto es de 0.14. Pero la probabilidad de que ocurran 10 llamadas por minuto es muy baja, en torno a 0.02.

Concepto de tráfico telefónico
El modelo de tráfico telefónico se compone de los siguientes elementos:
• un generador de llamadas de teléfono de M elementos

• que la probabilidad de que llegue una llamada a la central siga una distribución de Poisson

• un número de llamadas L

• una duración de llamada H

La intensidad de tráfico telefónico se mide en Erlang y se calcula de la siguiente manera para una hora (3.600 segundos):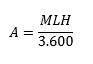   Por ejemplo, un solo teléfono que realice una llamada de 90 segundos de duración en una hora, tendrá un tráfico de:

Ahora volvamos al caso de la central telefónica. Si éstas tienen un número determinado de elementos de conmutación para atender llamadas, y en un momento dado están todas ocupadas, se dice que hay congestión o saturación, y las nuevas llamadas que intentan entrar se pierden. Se llama Grado de Servicio (GOS) al porcentaje de llamadas que se pierden por congestión.
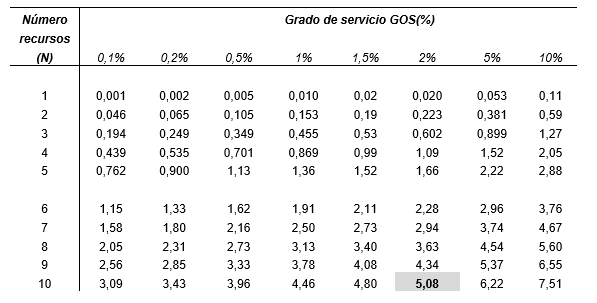
Para un sistema con las características que hemos descrito, el dimensionado de una central telefónica viene dado por la tabla Erlang B siguiente:

Como ejemplo, supongamos una central con 10 circuitos de conmutación y queremos que tenga un GOS del 2%, es decir que de 100 llamadas, 2 no pueden ser atendidas porque hay saturación.
Según la tabla anterior, la central es capaz de dar un servicio de 5,08 Erlangs. Si cada cliente consume 0,025 Erlangs como vimos en el ejemplo anterior, nuestra central será capaz de atender al siguiente número de clientes:

Por tanto, según el modelo de tráfico telefónico, con 10 circuitos de conmutación somos capaces de dar servicio a 203 clientes.

David Ortega, Doctor Ingeniero de Telecomunicación.